Bessels Korrektur
Die Bessel-Korrektur bezieht sich auf den n-1-Teil, der als Nenner in der Formel der Stichprobenvarianz oder Stichprobenverteilung verwendet wird.
Warum n-1?
Angenommen, n unabhängige Beobachtungen werden aus einer Grundgesamtheit mit Mittelwert (u) und Varianz (sigma) gezogen
2
). Im Allgemeinen sind sowohl (u) als auch (sigma) unbekannt und müssen geschätzt werden.
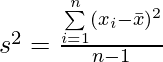
Der Stichprobenmittelwert schätzt den Populationsmittelwert (u) und die Stichprobenvarianz s 2 schätzt die Populationsvarianz (sigma 2 ). Idealerweise sollte mit (sigma 2 ) geschätzt werden
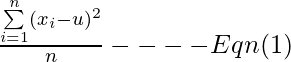
Da u nicht bekannt ist, erweist sich der Stichprobenmittelwert als der beste Schätzer, der verwendet werden kann. Somit
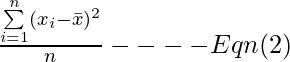
Problem: Das
Subtrahieren des Stichprobenmittelwerts in Gleichung (2) macht diese Summe so klein wie möglich, ungefähr muss der Stichprobenmittelwert in die Mitte der Beobachtungen fallen, während der Populationsmittelwert ein beliebiger Wert sein könnte. Die Summe in Gl.(2) wird also kleiner sein als die Summe in Gl.(1) , daher tendiert E qn(2) dazu, den wahren Wert der Populationsvarianz zu unterschätzen.
Lösung:
Um dies zu kompensieren, macht die Division durch n-1 die Stichprobenvarianz etwas größer als bei einer Division durch n. Es stellt sich heraus, dass es das Problem mathematisch richtig kompensiert.
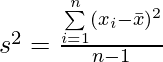
Im Durchschnitt entspricht dieser Schätzer der Populationsvarianz (Sigma 2 ), es ist hier nicht offensichtlich, warum hier (n-1) funktioniert, warum dieser Schätzer im Durchschnitt gleich der Populationsvarianz (Sigma 2 ) ist? Warum wird (n-2) oder (n-3) oder (n-0,5) nicht zur Division verwendet?
Wenn die Stichprobenstandardabweichung aus einer Stichprobe von n Werten berechnet wird, wird der Stichprobenmittelwert verwendet, der bereits aus derselben Stichprobe von n Werten berechnet wurde. Der berechnete Stichprobenmittelwert hat bereits einen der in der Stichprobe verfügbaren „ Freiheitsgrade der Variabilität“ (das ist der Mittelwert selbst) „aufgebraucht“. Für die Berechnung der Stichproben-Standardabweichung bleiben nur noch n-1 Freiheitsgrade der Variabilität übrig.
Beispiel:
Angenommen, 3 unabhängige Beobachtungen werden aus einer Grundgesamtheit gezogen, in der der Mittelwert der Grundgesamtheit (u) unbekannt ist. Wir finden, dass der Mittelwert der Stichprobe = 5 ist, und wir verwenden dies, um den Mittelwert der Grundgesamtheit (u) zu schätzen. Angesichts dieser Informationen können die ersten beiden Beobachtungen alles sein , nehmen wir an, sie sind 7 & 5.
| ich | x ich | x i -(sample_mean) |
|---|---|---|
| 1. | 7 | 7-5=2 |
| 2. | 5 | 5-5=0 |
| 3. | 3 | 3-5=-2 |
Wenn der Mittelwert der Beobachtung 5 ist und wir wissen, dass die ersten beiden Beobachtungen 7 & 5 sind, dann muss die dritte 3 sein und wir wissen, dass diese dritte Abweichung -2 sein muss, da sich alle Abweichungen vom Stichprobenmittelwert immer zu Null summieren .
Die dritte Beobachtung kann also keinen beliebigen Wert mehr haben, also bleiben hier nur zwei Freiheitsgrade übrig, sobald der Stichprobenmittelwert und zwei dieser drei Werte bekannt sind, wissen wir, was der dritte Wert sein muss, wir haben mit drei Graden von begonnen Freiheit, wenn wir drei unabhängige Beobachtungen aus der Population hatten, aber wir haben einen Freiheitsgrad verloren, als wir den Populationsmittelwert (u) mit dem Stichprobenmittelwert geschätzt haben. Daher nehmen wir zur Berechnung der Stichprobenvarianz(en 2 ) hier die Summe der quadrierten Abweichungen und dividieren sie durch die Freiheitsgrade (3-1).
Beim Schätzen der Varianz der Grundgesamtheit wird diese daher typischerweise durch die Freiheitsgrade geteilt, im Gegensatz zur Stichprobengröße, da dies zu einem besseren Schätzer führt.