Gauß-Seidel-Verfahren
Dies soll Jacobis Methode einen Schritt weiter bringen. Wo die bessere Lösung x = (x1, x2, … , xn) ist, wenn x1(k+1) eine bessere Annäherung an den Wert von x1 ist als x1(k), dann wäre es besser, wenn wir das Neue gefunden hätten Wert x1(k+1), um ihn (anstelle des alten Werts x1(k)) beim Finden von x2(k+1), … , xn(k+1) zu verwenden. Also wird x1(k+1) wie in Jacobis Methode gefunden, aber beim Finden von x2(k+1), anstatt den alten Wert von x1(k) und die alten Werte von x3(k),…, xn(k) zu verwenden , verwenden wir dann den neuen Wert x1(k+1) und die alten Werte x3(k), … , xn(k) und ähnlich zum Finden von x3(k+1), … , xn(k+1). Dieser Prozess, um die Lösung der gegebenen linearen Gleichung zu finden, wird als Gauß-Seidel-Verfahren bezeichnet
Das Gauß-Seidel-Verfahren ist eine iterative Technik zum Lösen eines quadratischen Systems aus n (n=3) linearen Gleichungen mit unbekanntem x.
Gegeben
Ax=B
, um das Gleichungssystem x zu finden, das diese Bedingung erfüllt.
Genauer gesagt sind A, x und b in ihren Komponenten: 
Dann ist die Zerlegung von A Matrix in ihre untere Dreieckskomponente und ihre obere Dreieckskomponente gegeben durch:

Das System der linearen Gleichungen wird umgeschrieben als:
Das Gauß-Seidel-Verfahren löst nun die linke Seite dieses Ausdrucks nach x auf, wobei der vorherige Wert für x auf der rechten Seite verwendet wird. Formaler kann dies geschrieben werden als:
Durch die Dreiecksform von L* können die Elemente von x(k+1) jedoch sequentiell unter Verwendung von Vorwärtssubstitution berechnet werden: 
Dieser Vorgang wird kontinuierlich wiederholt, bis wir die bessere angenäherte Lösung mit dem geringsten Fehler gefunden haben.
Beispiele:
Input : 3 4x+ y+ 2z= 4 3x+ 5y+ 1z= 7 x+ y+ 3z= 3 Output : [0, 0, 0] [1.0, 0.8, 0.39999999999999997] [0.6000000000000001, 0.9599999999999997, 0.48000000000000004] [0.52, 0.9919999999999998, 0.49600000000000005] [0.504, 0.9983999999999998, 0.4992000000000001] [0.5008, 0.99968, 0.49984] [0.5001599999999999, 0.9999360000000002, 0.4999679999999999] [0.500032, 0.9999872, 0.4999936] [0.5000064, 0.9999974400000001, 0.49999871999999995] [0.50000128, 0.999999488, 0.4999997439999999] [0.500000256, 0.9999998976000001, 0.49999994880000004] [0.5000000512, 0.9999999795199999, 0.4999999897600001] [0.50000001024, 0.999999995904, 0.499999997952] [0.500000002048, 0.9999999991808, 0.49999999959040003] [0.5000000004095999, 0.9999999998361601, 0.49999999991808003] [0.50000000008192, 0.9999999999672321, 0.49999999998361594] [0.500000000016384, 0.9999999999934465, 0.49999999999672307] [0.5000000000032768, 0.9999999999986894, 0.4999999999993445] [0.5000000000006554, 0.9999999999997378, 0.49999999999986894] [0.500000000000131, 0.9999999999999478, 0.49999999999997374] [0.5000000000000262, 0.9999999999999897, 0.49999999999999467] [0.5000000000000052, 0.9999999999999979, 0.49999999999999895] [0.5000000000000011, 0.9999999999999994, 0.49999999999999983] [0.5000000000000002, 0.9999999999999998, 0.5000000000000001] [0.49999999999999994, 1.0, 0.5] [0.5, 1.0, 0.5]
Angesichts der drei Gleichungen:
4x + y + 2z = 4 3x + 5y + z = 7 x + y + 3z = 3
Zuerst nehmen wir an, dass die Lösung der gegebenen Gleichung ist
(0,0,0)
Dann setzen wir zuerst den Wert von y und z in Gleichung 1 ein und erhalten den Wert von x und aktualisieren den Wert von x als
(x1,0,0)
Setzen Sie nun den aktualisierten Wert von x, also x1 und z=0, in Gleichung 2 ein, um y1 zu erhalten, und aktualisieren Sie dann unsere Lösung als
(x1,y1,0)
Setzen Sie dann endlich x1 und y1 in Gleichung 3 ein, um z1 zu erhalten, und aktualisieren Sie unsere Lösung als
(x1,y1,z1)
Wiederholen Sie nun denselben Vorgang weitere 24 Mal, um die Näherungslösung mit minimalem Fehler zu erhalten.
# Defining our function as seidel which takes 3 arguments # as A matrix, Solution and B matrix def seidel(a, x ,b): #Finding length of a(3) n = len(a) # for loop for 3 times as to calculate x, y , z for j in range(0, n): # temp variable d to store b[j] d = b[j] # to calculate respective xi, yi, zi for i in range(0, n): if(j != i): d-=a[j][i] * x[i] # updating the value of our solution x[j] = d / a[j][j] # returning our updated solution return x # int(input())input as number of variable to be solved n = 3 a = [] b = [] # initial solution depending on n(here n=3) x = [0, 0, 0] a = [[4, 1, 2],[3, 5, 1],[1, 1, 3]] b = [4,7,3] print(x) #loop run for m times depending on m the error value for i in range(0, 25): x = seidel(a, x, b) #print each time the updated solution print(x)
Ein Beispiel für die Matrixversion
Ein als Ax=b dargestelltes lineares System ist gegeben durch:
Wir wollen die Gleichung verwenden
Wo:
Wir müssen A in die Summe einer unteren Dreieckskomponente L* und einer strengen oberen Dreieckskomponente U zerlegen:
Die Umkehrung von L* ist:
Jetzt können wir die verbleibenden Dinge finden: 
Jetzt haben wir T und C und wir können sie verwenden, um die Vektoren x iterativ zu erhalten.
Zuerst müssen wir x{0} auswählen, wir können nur raten. Je besser die Schätzung, desto schneller arbeitet der Algorithmus.
Wir nehmen an: 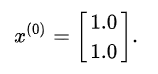
Dann können wir iterativ andere x{i}s berechnen: 
Jetzt kennen wir die exakte Lösung, die zu der oben berechneten Antwort passt. 
Tatsächlich ist die Matrix A streng diagonal dominant (aber nicht positiv definit).