Kollisionen in einer Dimension

Während des Spiels haben Sie vielleicht gesehen, wie zwei Billardkugeln miteinander kollidierten. Kollision ist das gewaltsame Zusammentreffen zweier unterschiedlicher Körper. Was passiert, wenn zwei Objekte kollidieren? Können wir die Geschwindigkeit oder Flugbahn der kollidierenden Körper identifizieren? Lassen Sie uns nachforschen!

Eine Kollision entsteht, wenn zwei Dinge für kurze Zeit miteinander in Kontakt kommen. Anders ausgedrückt ist ein Stoß ein kurzzeitiger gegenseitiger Kontakt zwischen zwei Massen, bei dem sich Impuls und Energie der kollidierenden Massen ändern. Sie haben vielleicht die Wirkung eines Stürmers auf Münzen gesehen, wenn sie beim Karambolagespiel kollidierten.

Restitutionskoeffizient

Das Verhältnis der Endgeschwindigkeit zur Anfangsgeschwindigkeit der wechselwirkenden Teilchen nach dem Auftreten einer Kollision zwischen ihnen wird als Restitutionskoeffizient bezeichnet. Der Restitutionskoeffizient wird mit „e“ mit einem Wert zwischen 0 und 1 bezeichnet. Da der Restitutionskoeffizient ein konstantes Gut ist, hat er keine Dimensionen. Es liefert mehr Informationen über die Elastizität der Kollision. Die perfekt elastische Kollision, bei der kein Verlust an kinetischer Gesamtenergie des Systems auftritt. Es ist im Grunde ein ganzzahliger Wert, der das Maß für die Beschaffenheit kollidierender Materialien darstellt.

Der maximale Wert des Restitutionskoeffizienten ist e = 1.

Die Formel für den Restitutionskoeffizienten lautet:

e = Relativgeschwindigkeit vor der Kollision / Relativgeschwindigkeit nach der Kollision

Wertebereich für z

Da der Restitutionskoeffizient zwischen 0 und 1 liegt, kann er folgenden Wertebereich enthalten:

Für e = 0 bezieht sich auf einen vollkommen unelastischen Stoß. Bei einer solchen Kollision geht maximale kinetische Energie verloren.
Wenn 0 < e < 1, bezieht sich dies auf eine reale unelastische Kollision, d. h. bei diesen Arten von Kollisionen geht etwas kinetische Energie verloren.
Wenn e = 1, bezieht sich auf einen vollkommen elastischen Stoß, bei dem keine kinetische Energie dissipiert wird. Die Objekte prallen mit der gleichen Geschwindigkeit ab, mit der sie sich einander nähern.

Kollisionsarten

Nach dem Impulserhaltungssatz gibt es beim Zusammenstoß von Objekten mit einzelnen Massen keinen Energieverlust. Es kann jedoch zu bestimmten Kollisionen kommen, ohne dass die Erhaltung der kinetischen Energie eingehalten wird. Basierend auf der Energieeinsparung, die bei Kollisionen verfolgt wird, können die folgenden Kategorien entwickelt werden:

(1) Elastischer Stoß

Elastische Stöße erhalten den Gesamtimpuls und die Gesamtenergie. Die gesamte kinetische Energie kann erhalten bleiben oder nicht. Da die bei der Kollision beteiligten Kräfte in der Natur konserviert sind, wird die Form der mechanischen Energie nicht in eine andere Energieform umgewandelt.

Nehmen wir zwei Objekte mit Massen m ₁ und m ₂ an, die sich mit den Geschwindigkeiten u ₁ bzw. u ₂ bewegen. Die Endgeschwindigkeiten nach dem Stoß dieser beiden Objekte seien v ₁ und v ₂ .

Nach dem Impulserhaltungssatz gilt:

m ₁ u ₁ + m ₂ u ₂ = m ₁ v ₁ + m ₂ v ₂

Nach der Erhaltung der kinetischen Energie:

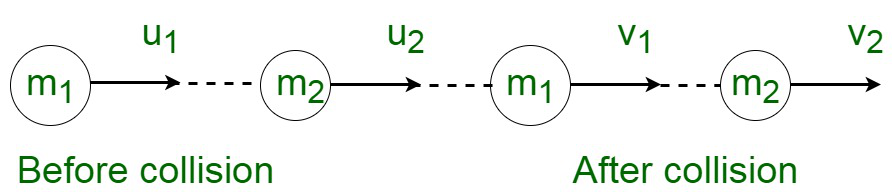
$\frac{1}{2} m_1u^2_1 + \frac{1}{2} m_2u^2_2 = \frac{1}{2} m_1v^2_1 +\frac{1}{2} m_2v^2_2$

Beispiele für elastische Kollisionen sind:

Die Kollision zwischen zwei Billardkugeln.
Einen Ball werfen und wieder auffangen.

Anwendungen der elastischen Kollision sind:

Die Kollisionszeit ist umgekehrt proportional zu der zwischen den wechselwirkenden Körpern wirkenden Kraft. Um die zwischen zwei Körpern wirkende Kraft zu maximieren, muss die Kollisionszeit verkürzt werden. Dasselbe ist für den anderen Fall möglich. Dies impliziert, dass zur Minimierung der Kraft zwischen zwei Körpern die Kollisionszeit erhöht werden muss.

Die Konzepte sind im Konzept der Einführung von Airbags in Fahrzeugen sichtbar. Die Idee ist, eine größere Kollapszeit bereitzustellen, um die Krafteinwirkung auf Objekte während einer Kollision zu minimieren. Airbags in Autos erreichen dies, indem sie den Zeitrahmen verlängern, der erforderlich ist, um den Schwung sowohl des Passagiers als auch des Fahrers des Autos zu stoppen.

(2) Unelastische Kollision

Inelastische Stöße erhalten den Gesamtimpuls und die Gesamtenergie. Die gesamte kinetische Energie kann erhalten bleiben oder nicht. Die Energie wird in andere Energieformen, also Wärme und Licht, umgewandelt. Die interagierenden Objekte können entweder aneinander haften oder beginnen, sich ausgerichtet in die gleiche Richtung zu bewegen.

Nach dem Impulserhaltungssatz haben wir

Da sich die Objekte in die gleiche Richtung bewegen, bewegen sich beide Objekte mit der gleichen Geschwindigkeit v,

m ₁ u ₁ + m ₂ u ₂ = (m ₁ + m ₂ )v

$v= \frac{m_1u_1 + m_2u_2}{m_1 + m_2}$

Die kinetische Energie der Massen vor dem Stoß ist: KE ₁ = $\frac{1}{2} m_1u^2_1 + \frac{1}{2} m_2u^2_2$
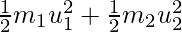
Die kinetische Energie nach dem Stoß ist: KE ₂ = 1/2 (m ₁ + m ₂ ) v ₂

Nach dem Energieerhaltungssatz gilt

$\frac{1}{2} m_1u^2_1 + \frac{1}{2} m_2u^2_2 = \frac{1}{2} (m_1+ m_2) v_2 + Q$

wobei sich „Q“ auf die Energieänderung bezieht, die zur Erzeugung von Wärme oder Schall führt.

Beispiele für unelastische Kollisionen sind:

Unfall von zwei Fahrzeugen.
Ein Auto prallt gegen einen Baum.
Der Ball fiel aus einer bestimmten Höhe und konnte nicht auf seine ursprüngliche Höhe aufsteigen.

Eindimensionale Kollision

Der Stoß, bei dem Anfangs- und Endgeschwindigkeit der beteiligten Massen auf einer Linie liegen. Alle an der Bewegung beteiligten Variablen treten in einer einzigen Dimension auf.

(1) Elastische eindimensionale Kollision

Bei elastischen Stößen bleiben Impuls und innere kinetische Energie erhalten. Denn elastische Stöße können nur mit mikroskopisch kleinen Teilchen wie Elektronen oder Neutronen simuliert werden. Betrachten Sie zwei Protonen mit den Massen m ₁ und m ₂

Nach dem Impulserhaltungssatz haben wir

m ₁ u ₁ + m ₂ u ₂ = m ₁ v ₁ + m ₂ v ₂

Wegen der Erhaltung der kinetischen Energie gilt

$\frac{1}{2} m_1u^2_1 + \frac{1}{2} m_2u^2_2 = \frac{1}{2} m_1v^2_1 +\frac{1}{2} m_2v^2_2$

Dies impliziert,

$m_1u^2_1 + m_2u^2_2 = m_1v^2_1 + m_2v^2_2$ (Ausklammerung 1/2)

Durch Umstellen erhalten wir: $m_1u^2_1- m_1v^2_1 = m_2v^2_2 - m_2u^2_2$

Deswegen,

$m_1(u^2_1- v^2_1)= m_2(v^2_2 - u^2_2)$

Bei der Erweiterung wird es,

$m_1(u_1+v_1 ) (u_1- v_1 )=m_2 (v_2 + u_2)(v_2 - u_2)$

Durch die Impulserhaltung:

$m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2$

Gruppieren mit denselben Massen:

$m_1u_1-m_1v_1 = m_2v_2 -m_2u_2$

Deswegen,

$m_1(u_1-v_1) = m_2(v_2 -u_2)$

Zur Division der beiden Gleichungen:

$m_1(u_1+v_1) (u_1- v_1) = \frac{m_2 (v_2 + u_2)(v_2 - u_2) }{ m_1(u_1-v_1 )} = m_2(v_2 -u_2 )$

Wir implizieren,

$u_1+v_1 = v_2 + u_2$

Jetzt,

$v_1 = v_2 + u_2- u_1$

Ersetzen des Wertes von $v_1$

$v_2 = \frac{[2 m_1 u_1 + u_2 (m_2-m_1)] }{ (m_1 + m_2 )}$ …….(1)

Verwenden Sie nun den Wert von v2 in der Gleichung $v_1 = v_2 + u_2- u_1$

$v_1 = \frac{[2 m_1 u_1 + u_2 (m_2-m_1)] }{ (m_1 + m_2)} + u_2- u_1\\ v_1 = \frac{[2 m_1 u_1 + u_2 (m_2-m_1) + u_2 (m_1 + m_2 ) - u_1(m_1 + m_2 )] }{ (m_1 + m_2 ) }$ …….(2)

Bei der Reduktion erhalten wir

$v_1 = \frac{[2m_2 u_2 + u_1 ( m_1 - m_2)] }{ (m_1 +m_2 )}$

Meistens tauschen diese Massen nach dem Zusammenstoß ihre Geschwindigkeiten aus. Wenn die Massen beider Körper gleich sind,

$v_1 = u_2\ and\ v_2 = u_1$

Falls das zweite Massenobjekt ruht und das erste Massenobjekt mit ihm kollidiert, kommt es nach dem Auftreten einer Kollision zu einer Vertauschung der Geschwindigkeiten, die erste Masse kommt zur Ruhe und die zweite Masse bewegt sich mit gleicher Geschwindigkeit zur ersten Messe.

Also $v_1$ = 0 und $v_2$ = $u_1$ . Falls $m_1 < m_2$ dann, $v_1 = -u_1\ and\ v_2 = 0$

Dies impliziert, dass der leichtere Körper (der Körper mit geringerer Masse) dazu neigt, mit seiner eigenen Geschwindigkeit zurückzuschießen, während die schwerere Masse an ihrer Position statisch bleibt.

Außerdem haben wir ggf.

$m_1 > m_2\ then\ v_1 = u_1\ and\ v_2 = 2u_1$

Einige Sonderfälle sind:

Fall I:

Bei Objekten gleicher Masse, d.h. $m_1 = m_2$

Unter Verwendung der Gleichungen (1) und (2) haben wir

$v_2=u_1, v_1=u_2$ .

Daraus können wir schließen, dass wenn zwei Körper gleicher Masse einen frontalen elastischen Stoß erleiden, es einen Geschwindigkeitsaustausch zwischen den Teilchen gibt. Auch der Impulsaustausch zwischen zwei Teilchen ist in diesem Szenario maximal.

Fall II:

Betrachten Sie das Zielteilchen in Ruhe, d.h $u_2=0$

Unter Verwendung der Gleichungen (1) und (2) haben wir

$v_2=\left(\frac{2m}{m_1+m_2}\right)u_1$ …..(3)

$v_1=\left(\frac{m_1-m_2}{m_1+m_2}\right)u_2$ ……(4)

Die Größe von transformiertem KE ist gegeben durch

$\frac{\frac{1}{2}m_2v^2_2}{\frac{1}{2}m_1u^2_1}=\frac{\frac{1}{2}m_2\left(\frac{2m_1u_1}{m_1+m_2}\right)^2}{\frac{1}{2}m_1u^2_1}\\$

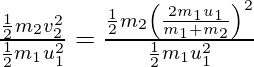
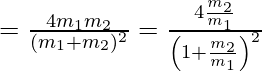$=\frac{4m_1m_2}{(m_1+m_2)^2}=\frac{4\frac{m_2}{m_1}}{\left(1+\frac{m_2}{m_1}\right)^2}$ ……(5)

wann $m_1=m_2$ , dann in diesem Zustand $v_0=0\ and\ v_2=u_1$

und ein Teil der KE übertragen werden würde

Daher werden nach der Kollision die jeweiligen Zustände und Geschwindigkeiten der Teilchen vertauscht, das erste Teilchen kommt zur Ruhe und das zweite Teilchen beginnt sich mit der Geschwindigkeit des ersten Teilchens zu bewegen.

In diesem Szenario, wo $m_1=m_2$ die Energieübertragung vollständig ist, sind das 100 %.

Und falls $m_1 > m_2$ oder $m_1 < m_2$ dann ist die Energieumwandlung nicht gleich 100%.

Fall III:

Wenn $m_2 >>>> m_1\ and\ u_2=0$

Unter Verwendung der Gleichungen (3) und (4) haben wir

$v_1 ≅ -u_1\ and\ v_2=0$ ……..(6)

Fall IV:

Wenn $m_1 >>>> m_2\ and\ u_2=0$

Unter Verwendung der Gleichungen (3) und (4) haben wir

$v_1 ≅ u_1\ and\ v_2=2u_1$ ………(7)

Deswegen,

Wir können daraus schließen, dass, wenn ein Teilchen mit einer größeren Masse eine Kollision mit einem vernachlässigbar leichteren Teilchen in Ruhe erfährt, das schwere Teilchen nach der Kollision die gleiche Geschwindigkeit beibehält und das leichte Teilchen die Bewegung mit einer Geschwindigkeit beginnt, die doppelt so hoch ist wie die eines schwereren Teilchens Massenobjekt.

(2) Unelastische eindimensionale Kollision

Der Impuls der beteiligten Teilchen bleibt erhalten, wodurch die kinetische Energie in verschiedene Energieformen umgewandelt wird.

Nach dem Impulserhaltungssatz haben wir

$m_1u_1 + m_2u_2 = (m_1 + m_2) v$

Da sich bei einer inelastischen eindimensionalen Kollision beide Objekte mit der gleichen Geschwindigkeit v bewegen, haben wir

$v = m_1u_1 + \frac{m_2u_2}{ m_1 + m_2}$

Der Verlust an kinetischer Energie kann gleichgesetzt werden mit:

$E = \frac{1}{2} m_1u^2_2 - \frac{1}{2} (m_1 + m_2) v_2$

Beispielproblem

Aufgabe 1. Ein Körper mit der Masse m, der sich mit der Geschwindigkeit V m/s bewegt, stößt mit einem anderen Körper zusammen, der das Doppelte seiner ursprünglich ruhenden Masse hat. Berechnen Sie das Verhältnis von KE vor und nach dem Stoß.

Lösung:

Masse des ersten Objekts = m
Masse des zweiten Objekts = 2m
Das Verhältnis von KE vor und nach der Kollision beträgt 9:1.

Aufgabe 2: Berechnen Sie den Restitutionskoeffizienten, wenn ein Gummiball aus 10 m Höhe von der Decke fällt. Er prallt zweimal ab und erreicht eine Endhöhe von 2,5 m.

Lösung:

Der Restitutionskoeffizient ist gegeben durch,
$e=\frac{Relative\ speed\ after\ collision}{Relative\ speed\ before\ collision}$
Beim Rechnen erhalten wir
$e =\frac{ 1}{\sqrt2}$

Aufgabe 3: Betrachten Sie zwei vollkommen elastische Teilchen A und B gleicher Masse m mit Anfangsgeschwindigkeiten von 15 m/sec bzw. 10 m/sec. Wie groß werden ihre Endgeschwindigkeiten sein?

Lösung:

Die Geschwindigkeiten der Körper werden sich nach dem Stoß austauschen, daher sind die Endgeschwindigkeiten der Massen
EIN B
10 fünfzehn

Aufgabe 4. Betrachten Sie einen Körper zunächst in der Ruhelage. Es beschleunigt ständig in eindimensionaler Bewegung. Erklären Sie den Zusammenhang zwischen der Verlustleistung und der Zeit.

Lösung:

Nach dem zweiten Bewegungsgesetz
v = u + bei
v = 0 + bei = bei
Da wir wissen, dass Macht gleichbedeutend ist mit ,
P = F × v
Daher haben wir,
P = (ma) × bei = ma ² t
Da m und n Konstanten sind,
Daher ist die Leistung direkt proportional zur Zeit.
P ∝ t.

Aufgabe 5: Betrachten Sie einen Körper zunächst in der Ruhelage. Es beschleunigt ständig in eindimensionaler Bewegung mit konstanter Kraft. Erklären Sie den Zusammenhang zwischen Weg und Zeit.

Lösung:

Denn wir wissen,
p = Kraft × Geschwindigkeit
[p] = [F] [v] = [MLT ^-2 ][LT ^-1 ]
[p] = [ML ² T ^–3 ]
L ² T ^–3 = konstant
⇒ $\frac{L^2}{T^2}$ = konstant
L ² ∝ T ³
⇒ L∝ $T^{\frac{3}{2}}$

Acervo Lima

Die größte Sammlung von Tutorials und Referenzen

Kollisionen in einer Dimension

Restitutionskoeffizient

Kollisionsarten

Eindimensionale Kollision

Beispielproblem

Latest posts

Restitutionskoeffizient

Kollisionsarten

Eindimensionale Kollision

Beispielproblem

Latest posts

Most popular posts