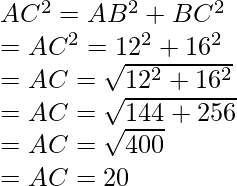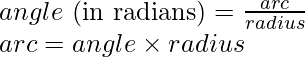In der Geometrie gibt es eine spezielle Klassifizierung, bei der Formen innerhalb anderer Formen zu finden sind, zum Beispiel ein Kreis innerhalb eines Dreiecks, ein Viereck innerhalb eines Kreises usw. Die Formen werden als eingeschrieben und umschrieben bezeichnet . Die innere Form ist als „Inscribed Shapes“ bekannt, während die äußere Form als „Circumscribed Shapes“ bekannt ist. Angenommen, ein Kreis ist in eine andere Form (ein Polygon) eingeschrieben, die Kanten des Polygons (die alle den Kreis berühren) sind die Tangenten an den Kreis.

Rechtwinklige Dreiecke, die in einen Kreis eingeschrieben sind 

Wenn ein Dreieck so in einen Kreis eingefügt wird, dass eine der Seiten des Dreiecks der Durchmesser des Kreises ist, dann ist das Dreieck ein rechtwinkliges Dreieck. 

Dies wird auch als Satz von Thales bezeichnet .

Nachweisen:

Dem folgenden Diagramm ist das OC-Liniensegment hinzugefügt. 

Da die Segmente OB, OC und OA alle Radien desselben Kreises sind, sind sie alle kongruent. Daher sind beide Dreiecke COB und COA gleichschenklige Dreiecke. Die Winkel B und BCO sind kongruent, da sie gegenüberliegende kongruente Seiten des gleichschenkligen Dreiecks COB sind. In ähnlicher Weise sind die Winkel A und ACO kongruent, weil sie gegenüberliegende kongruente Seiten des Dreiecks COA sind.

Die Summe der Maße der drei Winkel in einem Dreieck beträgt 180 Grad, also

m(∠A) + m(∠B) + m(∠C) = 180

Verwenden Sie die Winkeläquivalenzen aus dem vorherigen Absatz

m(∠C) = m(∠BCO) + m(∠ACO)



           = m(∠CBO) + m(∠CAO)

= m(∠B) + m(∠A)

Wenn wir dies in die vorherige Formel einsetzen, finden wir

2m(∠A) + 2m(∠B) = 180

und so ist m(∠A) + m(∠B) = 90. Da sich die Maße der drei Winkel des Dreiecks ABC zu 180 addieren, bedeutet dies, dass m(∠C) = 90° ist und somit das Dreieck ABC wie gewünscht ein rechtwinkliges Dreieck ist .

Frage: Das Dreieck ΔABC ist in einen Kreis O eingeschrieben, und die Seite AC geht durch den Mittelpunkt des Kreises. Finde den Durchmesser des Kreises.

Antworten:

 Wir wissen, dass das Dreieck, das einer Sehne eingeschrieben ist, die durch den Mittelpunkt des Kreises verläuft, ein rechtwinkliges Dreieck ist. 

Gegeben, BC = 16 und AB = 12. 



Hypotenuse Theorem kann hier angewendet werden, 

AC^{2}= AB^{2} + BC^{2} \\ = AC^{2} = 12^2 + 16^2 \\ = AC = \sqrt{12^2 + 16^2} \ \ = AC = \sqrt{144 + 256}\\ = AC = \sqrt{400} \\ = AC = 20

Der Durchmesser des Kreises ist 20. 

Eingeschriebene Winkel in Kreisen

Ein einbeschriebener Winkel in einem Kreis ist so definiert, dass seine beiden Seiten/Strahlen als Sehne zum Kreis wirken und der Scheitelpunkt des Winkels auf dem Umfang des Kreises liegt.

Wenn ein weiterer Winkel hinzugefügt wird, dessen Scheitelpunkt in der Mitte liegt und die Strahlen auf die Enden des vorherigen Winkels treffen, wird der Winkel, der durch den Mittelwinkel begrenzt wird, doppelt so groß wie der Winkel, der durch den anderen Winkel begrenzt wird.

Zyklische Vierecke

Wenn ein Viereck so in einen Kreis eingeschrieben wird, dass alle Eckpunkte des Vierecks den Umfang des Kreises berühren. Es gibt bestimmte Eigenschaften für das zyklische Viereck.

Eigenschaft: Die gegenüberliegenden Winkel eines zyklischen Vierecks addieren sich immer zu 180°. ODER Es kann gesagt werden, dass die entgegengesetzten Winkel ergänzender Natur sind. 

Hier ist ∠A + ∠C = 180°

 ∠B + ∠D = 180°

Wenn alle Winkel addiert werden, ist ∠A + ∠B + ∠C+ ∠D = 180 + 180 = 360°

Frage 1: Finden Sie in der Abbildung unten den anderen Winkel. 

Antworten: 

Da beide eingeschriebenen Winkel von demselben Bogen stammen, müssen die Winkel gleich sein. 

Der andere Winkel ist also auch 75 o

Frage 2: Finden Sie in der Abbildung unten die Länge des Nebenbogens AC. 

Antworten:

 Durch den zuvor untersuchten Satz wissen wir, dass der dem Kreis durch einen Bogen einbeschriebene Winkel die Hälfte des Winkels ist, der demselben Bogen in der Mitte einbeschrieben ist. Daher ist ∠AOC = 60°. 

Jetzt haben wir den Winkel in der Mitte eingeschrieben und der Radius des Kreises beträgt 4 cm (gegeben). 

Die Länge des Bogens kann durch ermittelt werden

 Winkel\text{ (im Bogenmaß)} = \frac{arc}{Radius} \\ arc = Winkel \times Radius \\

30° wird  \frac{\pi}{6}  im Bogenmaß angegeben. 

Setzen Sie also die Werte in die obige Formel ein. 

arc = \frac{\pi}{6} \times 4 \\ = \frac{4\pi}{6}\\ = \frac{4 \times 3.14}{6}\\ = \frac{12.56}{6} \\ = 2.0943

Die Länge des Bogens beträgt also 2,0943. 

Frage 3: In der gegebenen Abbildung ist CD die Sehne, die gleich dem Radius des Kreises ist, AB ist der Durchmesser wie gezeigt, die Sehnen AC und BD werden außerhalb des Kreises verlängert, um sich bei E zu treffen. Beweisen Sie, dass ∠AEB = 60°

Antworten: 

Zum Beweis: ∠AEB = 60°

Konstruktion: Verbinden Sie OC, OD und BC mit gepunkteten Linien.

Beweis: △COD ist ein gleichseitiges Dreieck, da alle drei Seiten gleich dem Radius des Kreises sind.

Also ∠COD= 60° und ∠CBD = 30° (halber Winkel in der Mitte)

Bei △ACB ist ∠ACB = 90°

∠BCE= 180-90 (da AE eine Gerade ist) = 90°

In △BCE ist ∠BEC+ 90+ 30 = 180°

∠BEC = 60°

Daher ist ∠AEB = 60°